Understanding Leetcode Prefix Sum Pattern

Detail analysis of prefix sum pattern

Introduction

The Prefix Sum pattern is a common technique used in algorithms to solve problems involving subarrays, sums, and ranges more efficiently. It allows to preprocess an array and then quickly calculate the sum of elements in any subarray or find specific patterns such as balanced subarrays. This technique is particularly useful in problems where you need to calculate sums repeatedly over different ranges of an array.

What is Prefix Sum?

A prefix sum is an array where each element at index `i` stores the cumulative sum of the elements from the start of the array up to index `i`. In other words, for an array `nums[]`, the prefix sum at index `i` is:
prefix[i] = prefix[i-1] + arr[i] for i > 0

Suppose we have an array [1, 2, 3, 4, 5]. The prefix sum array would be [1, 3, 6, 10, 15]. If we need to find the sum of elements between index 1 and 3, we calculate:

• sum(1, 3) = prefix[3] - prefix[0] = 10 - 1 = 9.

This allows for quick retrieval of subarray sums, which can help solve various problems.

Key Use Cases for Prefix Sum:

1. Subarray Sum Problems:
— In many problems, we’re asked to find the sum of elements in a subarray, or we may be asked to check for a subarray that satisfies a particular condition (e.g., the sum equals a target).
— Prefix sums help reduce the time complexity of finding the sum of any subarray from O(N) to O(1) by simply subtracting two precomputed values.

2. Subarrays with Target Sum:
— In problems where we need to find subarrays whose sum equals a specific target, we can use prefix sums combined with a hash map to track previously seen sums and quickly identify whether a subarray with the desired sum exists.

Prefix Sum Pattern in LeetCode

Here are a few common LeetCode problems where the prefix sum pattern is used:

1. Subarray Sum Equals K (LeetCode #560):
— Problem: Given an array of integers and an integer `k`, find the total number of continuous subarrays whose sum equals `k`.
— Approach: Use a hash map to store the cumulative sums at each index. If the difference between the current cumulative sum and `k` has been seen before, it means there’s a subarray that sums to `k`. This reduces the time complexity to **O(N)**.

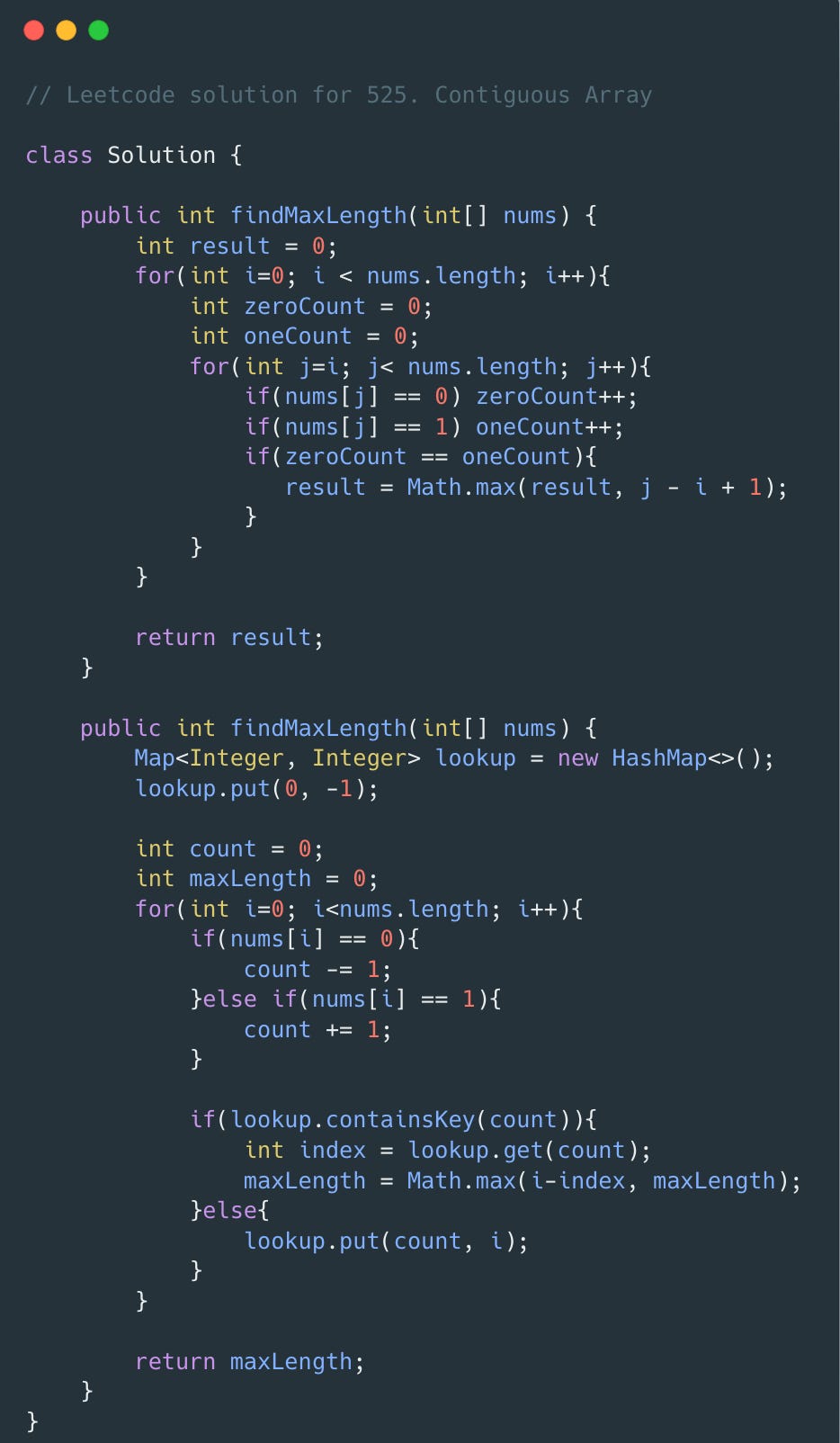
2. Find the Maximum Length of a Subarray with Equal 0s and 1s:
— Problem: Given a binary array, find the maximum length of a contiguous subarray with equal numbers of `0`s and `1`s.
— Approach: Convert `0`s to `-1`s and use prefix sums to find subarrays whose sum is `0` (indicating an equal number of `0`s and `1`s). A hash map stores the first occurrence of each prefix sum, helping track the start and end of the longest balanced subarray.

3. **Range Sum Query (LeetCode #303)**:
— Problem: Given an integer array `nums`, implement the `sumRange` function that returns the sum of elements between two indices `i` and `j`.
— Approach: Compute the prefix sum array during initialization, and then for each query, calculate the sum in **O(1)** time using the difference of prefix sums.

4. Continuous Subarray Sum (LeetCode #523):
— Problem: Given an integer array and a target `k`, find out if there is a continuous subarray whose sum is a multiple of `k`.
— Approach: Use the prefix sum pattern to track cumulative sums modulo `k`. If two cumulative sums have the same remainder when divided by `k`, the subarray between them has a sum that is divisible by `k`.

Prefix Sum with Hash Map:

In many LeetCode problems, prefix sums are combined with hash maps for faster lookups. The hash map stores the first occurrence of each prefix sum, which helps to determine whether a subarray with a particular sum exists quickly.

Here’s how this works:
1. Maintain a running sum (prefix sum) while traversing the array.
2. For each element, check if the difference between the current prefix sum and the target (or some condition) has been seen before in the hash map.
3. If yes, it means a subarray that satisfies the condition has been found.
4. If not, store the current prefix sum in the hash map for future reference.

Example of Prefix Sum with Hash Map:

For the problem Subarray Sum Equals K(LeetCode #560), we can use this approach:

public int subarraySum(int[] nums, int k) {
   Map<Integer, Integer> prefixSumCount = new HashMap<>();
   prefixSumCount.put(0, 1); // Initialize with 0 prefix sum
   int count = 0, prefixSum = 0;
 
   for (int num : nums) {
     prefixSum += num; // Update prefix sum
     if (prefixSumCount.containsKey(prefixSum - k)) {
        count += prefixSumCount.get(prefixSum - k); // Found a valid subarray
     }
     
     prefixSumCount.put(prefixSum, prefixSumCount.getOrDefault(prefixSum, 0) + 1); // Store current prefix sum
   }
 
   return count;
}

Benefits of the Prefix Sum Pattern:
Efficiency: It reduces the time complexity of finding subarray sums to O(1) after preprocessing.
Simplicity: The pattern is easy to apply once you understand the mechanics of prefix sums and cumulative sums.

Conclusion

The Prefix Sum pattern is a versatile and powerful technique for solving array-based problems involving subarray sums, range queries, and balance conditions. By preprocessing the array to compute cumulative sums and using hash maps for efficient lookups, you can significantly reduce the time complexity of many problems. Understanding and mastering this pattern is essential for efficiently solving a wide range of problems on platforms like LeetCode.